Özet
Bu yazı1 Galileo’nun “Doğanın dili matematiktir” sözünü ve Poincaré’nin yalınlığı bilimin bir önkoşulu olarak gördüğünü hatırlatarak başlamaktadır. Müziğin doğa ile iletişimde en estetik araç kabul edilebileceği belirtilmektedir. Yalınlığa pür matematik örnek olarak verilmekte ve Pisagor ile Zarlino ses sistemleri bu bağlamda anlatılmaktadır. Poincaré’nin “Basit görünen şey yeniden karmaşık bir yapıya dönüşebilir” karşı tezine de mekanik öğrenme örnek olarak verilmektedir. Müziğin uygulamalı matematikle ilintisi Fourier teoremi ve vurular gibi örneklerle anlatılmaktadır. Bu yazı Türk musikisindeki makam olgusuna hesaplamalı bir yaklaşım ile sona ermektedir. Buna göre iki makam arasındaki, iki eser arasındaki ve bir eserle bir makam arasındaki uzaklık, bir sayı ile gösterilebilmektedir.
Giriş
Müziğin matematikle yakından ilişkili olduğu hep söylenegelmiştir. Bunun en çarpıcı örneği, Ortaçağ üniversitelerinde mutlaka bulunan dört fakültenin aritmetik, müzik, astronomi ve geometri (tek sözcükle: quadrivium) olmasıdır. 2 Müziğin pür matematik ile ilişkisi bağlamında yorumlanabilecek bu olgu daha sonra konservatuvar türü müzik eğitimlerinde görünür olmaktan çıkmıştır. Ancak bir yandan hâlâ müzik teori tarihi alanındaki çalışma konularından biridir, öte yandan günümüzde mekanik öğrenme (machine learning) disiplininin yaygınlaşması, hesaplamalı müzikoloji ve hesaplamalı müzik teorisi adı verilen yeni araştırma alanları oluşmasına yol açmıştır. Bu, kanımızca müziğin pek çok alanında matematiğin (ama bu kez uygulamalı matematiğin) tekrar boy göstermeye başlaması demektir.
Bu çalışmada matematik ile müzik ilişkisi olabildiğince Türk müziğiyle ilgili çalışmalar zemininde gözden geçirilecektir.
Doğanın dili
5 yüzyıl önce Galileo (1564 – 1642)’nun söylediği şu söz iyi bir hareket noktasıdır:

Şekil 1. Galileo (1564 – 1642)
“Evreni anlamak istiyorsanız önce yazıldığı dili öğrenmelisiniz… Evren matematik dili ile yazılmıştır.”
Bu sözü şöyle dile getirenler de olmuştur:
“Doğanın muazzam kitabının dili matematiktir.”
Demek ki doğayla ancak matematik dili kullanılarak doğrudan iletişim kurulabilir. Bu iletişimin en estetik biçimi de müzik olsa gerektir.
Yalınlık
Matematikçi ve fizikçi Henri Poincaré (1854-1912), farklı bilim yapma biçimlerinden bahsetmiş ve fizik (bilim) tarihinin, birbirine zıt iki yönelim içinde olduğunu gösterdiğini savunmuştur:

Şekil 2. Henri Poincaré
“Bunlardan ilkinde, birbirinden ayrı kalacaklarmış gibi görünen şeyler arasında yeni bağlar keşfedilir ve böylece dağınık olan olaylar bir araya gelerek bir bireşim halinde düzenlenirler. Bu sayede bilim yalınlığa, birliğe doğru ilerler. Yalınlığın güzel olması yüzündendir ki genellikle yalın olgular, büyük olguları araştırmak için seçilmektedir.”3
Yalın → Karmaşık → Yalın süreci
Bu ünlü bilim insanı, ikinci yönelimde tersine bir süreç işlediğini savunur. Buna göre her gün yeni gözlemler yapılması sayesinde yeni olgular ortaya çıkmaktadır. “Bunların durumunun netleşmesi için ise uzun bir süre beklemek gerekecektir. Bu süreçte kimi zaman basit görünen şey yeniden karmaşık bir yapıya dönüşebilir. Bu ise bilimin, çeşitliliğe / karmaşıklığa doğru gittiği düşüncesine neden olabilir.”4
Poincaré, ardından, bilimin yalınlık yönelimi baskın çıkarsa mümkün olacağını ekler.
Mekanik öğrenme tekniklerinin müziğe uygulanma evresi kanımızca bu ikinci yönelim kapsamına girmektedir. Geniş veritabanları üzerinden ‘öğrenme’, bu karmaşık yapının iyi bir örneğidir. Ancak, bu sayede ulaşılan çıkarımlar yeni yalın örüntülerin keşfedilme potansiyeline de sahiptir.
Müzik
Bu kısımda, Poincare’nin öngördüğü ‘bilim yapma’ biçimlerinin uygulanabileceği alanlardan birinin müzik olduğuna ilişkin argümanlar sergilenmeye çalışılacaktır. Dolayısıyla müziğin pür matematikle ilgili ve yalınlığa yönelik boyutundan başlıyoruz…
Müzik, belli tınılara sahip bir dizi sesin art arda ya da aynı anda çeşitli frekanslarda, çeşitli sürelerle ve çeşitli gürlüklerde üretilmesiyle oluşur. Sesler art arda işitiliyorsa ezgisel/melodik, aynı anda işitiliyorlarsa uygusal/armonik yapıdadırlar. Sesin bileşenlerinden en önemlisi, frekanstır.
Peki, ‘iyi’ bir ezgisel motif ya da bir akor için, üretilen seslerin frekansları arasında nasıl bir bağıntı bulunmalıdır?
Kuşkusuz rasgele bileşimlerin büyük çoğunluğu kötü sonuçlar verecektir. Bu gerçek en az bin yıldır bilinmektedir. Örneğin İbn Sînâ (980 – 1037), iki sesin oluşturduğu müzikal aralığın 34/33 ile ifade edilen orandan küçük olması durumunda kulağın bu aralıkları sağlıklı bir şekilde ayırt edemeyeceğini dile getirmiştir.5
Buna karşılık, Pisagor diyatonik dizisi kulağa hoş gelir (bkz. Şekil 3).
Şekil 3. Pisagor diyatonik dizisi
Notaların altlarındaki rasyonel sayılar, her bir notanın referans sesi ile oluşturdukları müzikal aralıkları göstermektedir. Örneğin temel ses Do’nun frekansı bilimsel perde 6 standardının öngördüğü 256 Hz’e akort edilmişse La’nın frekansı
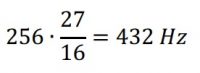
demektir.
Bu bağıntı ters yönde de işler. Örneğin La’nın frekansı günümüzde geçerli standarttaki gibi 440 Hz alınırsa Do’nun frekansı şöyle hesaplanır:
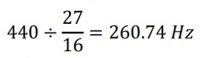
Zarlino diyatonik dizisi ise özellikle çokseslilikte öne çıkar (bkz. Şekil 4).
Şekil 4. Zarlino diyatonik dizisi
Bu ‘iyi olma’ ya da ‘hoşa gitme/gitmeme’ olgusunun altında yatan nedenleri araştırmakta yarar olduğu açıktır.
Pisagor dizisi
İlk dizi ile başlayalım. Çünkü o, kronolojik bakımdan önce ortaya çıkmıştır ve hem müzikal gerekçe hem matematik olarak en yalın yapıya sahip dizidir. İçerdiği seslerin bağıl frekansları şu formülle belirlenmiştir:

Matematiğin (yani evrenin) diliyle yazılmış bu ifadenin sözel müzik diline çevrilmiş biçimi şudur:
Bu yolla elde edilen dizideki sesler arasında tam beşli aralıkları vardır.
Pisagor dizisinin elde edilme sürecinde kilit rol oynayan ve 3/2 oranıyla ifade edilen tam beşli aralığı, ünison (1/1) ve oktavdan (2/1) sonra gelen en derli müzikal aralıktır. 7 Ayrıca ünison ve oktavın aksine, müzikal olarak zengin bir aralıktır.
Diziye Fa notası ile başlanırsa şu nota ve bağıl frekans dizisi elde edilir:
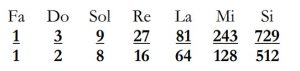
(Mod operatörünün gereği olarak, çarpımların sonucu 2’den büyük olduğunda elde edilen değer 2’ye bölünmektedir.)
Diziyi Do’dan başlatmak amacıyla, her bir terimi 3/2’ye bölelim:

Bütün notaları aynı oktavda toplamak amacıyla, değeri 1’den küçük terimleri 2 ile çarpalım:

… ve diziyi küçükten büyüğe sıralayalım. İşte notası Şekil 3’de gösterilen Pisagor diyatonik dizisi budur:

Matematiksel ifadesi ve müzikal gerekçesi çok yalın olan bu dizi, müzik tarihi boyunca en etkili iki ses sisteminden biri olmuştur. Başta Türk makam müziği olmak üzere bazı geleneksel müzikler üzerindeki etkisi halen sürmektedir.
Pisagor dizisini elde etme sürecinin ilginç özelliklerinden bir başkası da, terim sayısının 7 ile sınırlı olma zorunluluğu bulunmamasıdır. Örneğin 5 adım daha ilerlenirse (n=1,2…,7,8,9,10,11), 1 oktavda 12 nota içeren kromatik dizi elde edilir. Türk makam müziğinde önemli iki kilometre taşı olan 17 perdeli Safiyyüddin Urmevi ses sistemi ile 24 perdeli Arel – Ezgi – Uzdilek ses sistemi, Pisagor yönteminin 7 ya da 12 değil, sırasıyla 17 ve 24 adım uygulanmasıyla elde edilmiştir.8Üstelik adım sayısının sonsuza kadar ilerletilebilmesi derin bir matematiksel ve müzikal anlama sahiptir. Bunun matematiksel boyutu Müzisyenler Denklemi diye anılır:
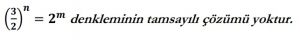
Bu olgu, müzik diliyle şöyle ifade edilebilir:
Temel bir sesten başlayıp tam beşli aralıklarıyla ne kadar ilerlenirse ilerlensin, temel sesin eşdeğerine ulaşılamaz.
Doğal dizi ya da Zarlino dizisi
İkinci sisteme geçelim. Bu dizideki seslerin Hertz (Hz) cinsinden frekansları günümüzde geçerli standarda göre saniyedeki titreşim sayıları, La 440 Hz temel alınmak üzere belirlenirse şu dizi elde edilir:
![]()
Bu dizide bir örüntü aramak ilginç sonuçlar verecektir. Önce ardışık terimler arasındaki farklara bakalım:
![]()
Dört farklı değer var. Tüm terimleri, bunların ortak bölenlerinin en büyüğü (EBOB) olan 11’e bölelim:
![]()
2, 3 ve 5 asal sayılarının yer aldığı bir örüntü olduğu anlaşılıyor. Fakat daha ileri gidilemiyor.
Bu kez ardışık elemanlardan, sonrakini öncekine oranlayıp sadeleştirelim:
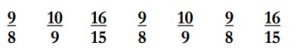
Bu kez üç farklı değer var. 2, 3 ve 5 asal sayılarıyla ilgili bir örüntü yine görülüyor: Pay ve paydalardaki sayılar çarpanlarına ayrılırsa bu üç asal sayı elde ediliyor.
Tüm seslerin frekanslarının ilk sesin frekansına oranlarına bakalım:

2, 3 ve 5 yine dikkati çekiyor.
Bu son elde edilen rasyonel sayı dizisi, doğal sistem ya da Zarlino sistemindeki
Do Re Mi Fa Sol La Si Do
nota dizisine ait bağıl frekanslardır.
Müzik teori tarihindeki ses sistemlerinin ikinci kilometre taşlı bu dizidir. Pisagor sistemi yüzyıllarca hemen hemen tek seçenek olmuştur. İlkin Batlamyus (Ptolemy) tarafından öngörülen doğal dizi ise Ortaçağ Avrupasında armoni öne çıkıp üçlü ve altılı müzikal aralıklar önem kazanınca tekrar gündeme gelmiş, Zarlino tarafından yapılan iki küçük değişiklikten sonra temel ses sistemi olmuştur.
Bu iki dizi karşılaştırılınca üç terimde niceliksel olarak küçük bir fark görülür:
Pisagor:

Zarlino:

Farklı olan üç terim için de, Pisagor(i) / Zarlıno(i) oranı 81/80’dir. Örneğin:
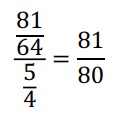
Bu küçük değer sentonik koma olarak anılır.
Ama müzikal açıdan, özellikle çoksesli müzikte, fark ihmal edilecek gibi değildir.
Bu iki dizideki pür matematik açısından en temel fark, perde ve aralıkları temsil eden rasyonel sayıların pay ve paydalarındaki tamsayılar çarpanlarına ayrılınca görülür: Pisagor sistemindeki en büyük asal çarpan 3 iken, Zarlino sistemindeki en büyük asal çarpan 5’tir. Önemsiz görülebilecek bu fark, armoniye geçişin zorunlu bir sonucu olarak ortaya çıkmıştır. Bu sayede, örneğin özellikle çoksesli müzikte önemli bir müzikal aralık olan büyük üçlü, Zarlino sisteminde 5/4 oranıyla ifade edilebilmektedir. Oysa aynı aralık Pisagor sisteminde 81/64 oranı ile ifade edilir… Yalınlık!
Fourier Teoremi
Yavaş yavaş, mühendislik matematiğine giriyoruz…
Müzik aletlerinin ürettiği sesler analiz edilince, bunların farklı frekans, genlik ve fazda birtakım seslerin bileşiminden oluştuğu görülür. Bu amaçla en yaygın kullanılan teknik, Fourier analizidir. Armonik yapıda çalgıların ürettiği sesler için şu özellik söz konusudur:
Çıkan sesin temel titreşim frekansı f ise, onun yanısıra 2f,3f,4f,5f,… frekanslı sesler de işitilir. Armonikler denilen bu bileşenlerin indisleri ile genlikleri -çeşitli ağırlıklarla- ters orantılıdır. Yani armonik seslerin numaraları büyüdükçe, bileşke ses içindeki işitilebilirlikleri azalır.
Pisagor ve Zarlino sistemleri bu bağlamda karşılaştırıldıklarında, Zarlino sisteminde 5. armoniğin de hesaba katıldığı, Pisagor sisteminde ise 3. armonikten sonrasının dikkate alınmadığı görülür. Bir başka deyişle, telli bir çalgıdan çıkan sesin bileşenleri dijital olarak sonsuz terimli şu formülle gösterilebilir iken9
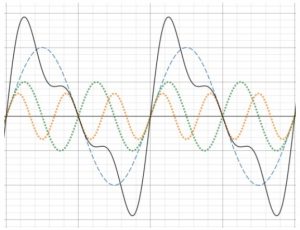
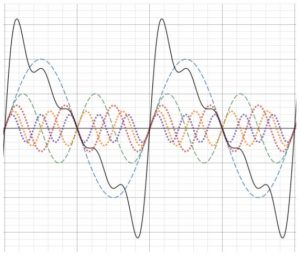
Pisagor sistemi bu terimlerden yalnızca ilk 3’ünü (bkz. Şekil 5), Zarlino sistemi ise ilk 5’ini (bkz. Şekil 6) dikkate almış gibidir.
Şekil 5. Frekansları f, 2f, 3f (kesikli ve noktalı mavi, yeşil ve kırmızı eğriler) basit sesler ve bunların bileşkesi (sürekli siyah eğri).
Şekil 6. Frekansları f, 2f, 3f, 4f, 5f (kesikli ve noktalı eğriler) basit sesler ve bunların bileşkesi (sürekli eğri).
Logaritma ve Tamperaman
Türk makam müziğinin resmî ses sistemi olan ve Arel – Ezgi – Uzdilek üçlüsünün adlarıyla anılan sistemin matematiksel – fiziksel temellerini atan Ord. Prof. Salih Murat Uzdilek, musikiyi üç döneme ayırır:
- Din ve halk musikileri devri,
- Armoni başlangıcı,
- “Bach’ın tervic ettiği (kabul ettirdiği, değerini artırdığı) eşit tamperamanlı gam.”
Uzdilek, bu 3’üncü dönemi logaritmanın keşfi (1614) ile ilişkilendirir.10
Ses sistemleri konusunda da çalışan ve eser veren iki müzik insanı -Abdülkadir Töre ve Ekrem Karadeniz- de şunu yazmışlardır:
“Dünyanın en yaygın müzikal çalgılarından olan piyano, logaritmanın keşfinden sonra bugünkü sistemine kavuşabilmiştir.” 11
Müzik için bu derecede önemli olan logaritma fonksiyonunun 2 tabanına göre olanı kullanılır. Çünkü 2 sayısı oktavı (sekizliyi) temsil eder ve birbiriyle oktav aralığı oluşturan sesler aynı sınıftandır.
Tamperaman, notaların frekanslarında bazı küçük değişiklikler yapılmak suretiyle müziği, çalgıları yalınlaştırmayı hedefler. Kimi yazarların yedirim olarak Türkçeleştirdiği tamperaman, logaritma ile yakından ilişkilidir. Özellikle eşit tamperaman 12 için gerekli hesapları, logaritma olmadan yapmak neredeyse olanaksızdı. Örneğin oktavın işitsel olarak eşit 12 parçaya bölünmesiyle elde edilen yarı-ton adlı müzikal aralığın değeri ’![]() ‘dir ve bunu (2 tabanına göre) logaritma olmadan hesaplamak neredeyse olanaksızdır:
‘dir ve bunu (2 tabanına göre) logaritma olmadan hesaplamak neredeyse olanaksızdır:
![]()
f1ve f2 frekanslı seslerin oluşturduğu yarı-ton cinsinden aralık şöyle hesaplanır:
![]()
Bu denklem 12TET’teki ardışık sesler için yazılırsa
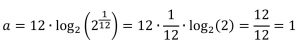
elde edilir. Yani 12TET’teki tüm ardışık sesler arasında 1 yarı-ton aralığı vardır.
Eşit tamperamanlı sistemlerde herhangi bir sesle oktavlarının oluşturduğu aralıklar dışındaki tüm aralıklar ancak irrasyonel sayılarla ifade edilebilir. Rasyonel sayı olarak ifade edilebilen örneğin 440 Hz ve 495 Hz frekanslı seslerin oluşturduğu müzikal aralık, yarı-ton cinsinden şöyle hesaplanır:
![]()
Vurular
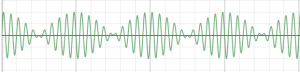
f ve f+∆f frekanslı (yani frekansları birbirlerinden ∆f gibi küçük bir miktar kadar farklı) iki ses aynı anda üretildiklerinde, frekansı bu iki sesin frekanslarının ortalaması olan bileşke bir ses işitilir. Fakat bundan da ilginç bir başka fiziksel olgu daha ortaya çıkar: Bu küçük farktan dolayı bir genlik dalgalanması oluşur. Bu fiziksel olguya (birinci tür) vuru adı verilir (Şekil 7).
Şekil 7. Birinci tür vuruların grafiği
Bu olgunun ‘evrenin dilindeki’ ifadesi, (matematik bilmeyenlerin gözünü korkutacak görünümde olsa da) hiçbir tereddüde mahal vermeyecek netliktedir:
Formülün yalınlığına karşılık, yukarıda sözü geçen ortalama frekans ve dalgalanma olguları eşitlikte tartışma götürmez biçimde görülmektedir:
- Sinüslü terimin argümanındaki (f +∆f/2), iki frekansın ortalamasından ibarettir.
- Kosinüslü terim ve 2 ile çarpımı ise genlikteki değişkenliği temsil eder; iki sesin frekansları farkının yarısı bir periyoda sahip bir dalgalanma yaratır.13
Birlikte tınlayan iki sesin frekansları arasında oktav + ∆f gibi bir fark varsa algısal bir olgu olan ikinci tür vurular oluşur.
İşitsel test
Bu yazıda sözü geçen üç ses sistemi (Pisagor, Zarlino ve 12TET) için Do Majör gamı basit seslerle (sinüs dalgalarıyla) sentezlenmiş, böylelikle sözel açıklamalar işitsel olarak pekiştirilmeye çalışılmıştır.
Üç sistem için de referans nota olarak dördüncü oktavdaki 440 Hz frekanslı La alınmıştır. Öteki notaların frekansları, sistemlerin yukarda verilen aralık yapılarına göre hesaplanmıştır (bkz. Şekil 8).
Şekil 8. Pisagor, Zarlino ve 12TET sistemlerindeki Do Majör gamının frekansları ve tek tek, ikili ikili ve üçü birlikte seslendirme örneği
Bu dizileri art arda dinleyerek frekans farklarını algılamak yetenek ve eğitim gerektirebilir. Ancak şeklin ikinci sütununda görüldüğü gibi notaları aynı anda dinleyince, oluşan birinci tür vurular nedeniyle bu kez farkları algılamamak olanaksızdır. Hatta vurular sayılıp her notanın 2 saniye sürdüğü hesaba katılarak, aynı anda işitilen iki sesin frekans farkının kaç Hz olduğunu söylemek bile mümkün hale gelir. Örneğin Zarlino sistemindeki Sol ile 12TET sistemindeki Sol’ün frekans farkı 396-392=4 Hz’tir; çünkü bu iki notanın aynı anda işitildikleri süre zarfında 8 vuru oluştuğu duyulmaktadır.
Ses örneğini dinlemek için şu adresi ziyaret ediniz:
https://freesound.org/people/mus2a/sounds/479332/
Zarlino ile Pisagor sistemlerindeki Fa’ların frekanslarının (sırasıyla 352 Hz ve 347.7 Hz) farkı 4.3 Hz’dir. Zarlino ile 12TET Fa’larının (352 ve 349.2 Hz) farkı ise 2.8 Hz’dir. Farkların farkı olan 1.5 Hz’in dünya müzik teorisi tarihinin yörüngesini belirlediği söylenebilir. Çünkü Fa ile, örneklerimizde referans ses aldığımız La notaları arasında büyük üçlü aralığı vardır ve bu aralığın en doğal değeri tam olarak Zarlino sistemindekidir. Pisagor sistemi yürürlükteyken, yani Batıda armoniye henüz geçilmemişken kullanılagelen Fa’nın peslik derecesi, armoni ile birlikte kulakları rahatsız etmeye başlamış, o nedenle Fa’sı 4.3 Hz daha tiz olan Zarlino sistemi kullanılmaya başlanmıştır. Öte yandan, günümüzde Batıda armoninin ağırlığı sürdüğü halde artık 12TET sistemi kullanılmaktadır. Bunun nasıl olabildiğinin cevabı muhtemelen şurada gizlidir:
12TET Fa’sı Zarlino Fa’sına, Pisagor Fa’sı – Zarlino Fa’sı mesafesinden 1.5 Hz daha yakındır. Yani kulaklar 2.8 Hz farkı tolere etmiş, 4.3 Hz farkı ise reddetmiştir. 14
Görsel
Vuru olgusu, Batıda armoniye geçişle birlikte Pisagor dizisinin neden terkedildiğine de açıklık getirir: Melodilerde önemli bir sorun oluşturmayan Pisagor üçlüsü ve altılısı aralıkları, armonik yapılarda rahatsızlık yaratır. Örneğin telli bir çalgının ürettiği 256 Hz frekanslı sesin 5. armoniği (256 ∙ 5 =) 1280 Hz, bunun iki oktav pesi (referans sesle doğal büyük üçlü aralığı oluşturan ses) 1280 / 4 = 320 Hz’tir. 5. armonik genellikle işitilebilir bir genliğe sahiptir. Durum böyleyken temel sesle Pisagor büyük üçlüsü (81/64) aralığı oluşturan (256 ∙ 81/16 =) 324 Hz frekanslı nota ile bir akor seslendirilirse ∆ = 324 – 320 = 4 değeri nedeniyle vurular algılanır ve bu da rahatsız edici bir etkiye sahiptir.
Birlikte tınlayan iki sesin oluşturduğu müzikal aralığın yalın bir rasyonel sayı ile ifade edilebilir veya edilemez oluşu (hatta irrasyonel bir sayıdan oluşması) görsel olarak bir Lissajous eğrisi ile temsil edilebilir. Seslerden birinin sinyali osiloskopun süpürme devresine, ötekininki düşey saptırıcıya gönderilince ekranda oluşan görüntü, değerler parametrik denklem formunda yerlerine yazılıp çizdirilmekle elde edilen grafikle aynı görünüme sahiptir (bkz. Şekil 9).
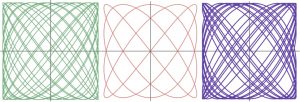
Şekil 9. Solda birbiriyle Pisagor büyük üçlüsü (81/64), ortada doğal büyük üçlü (5/4) ve sağda tampere büyük üçlü (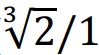 ) aralıkları oluşturan ikişer basit sesin Lissajous eğrileri
) aralıkları oluşturan ikişer basit sesin Lissajous eğrileri
Oranların kesirli sayı karşılıkları (sırasıyla 1.2656, 1.25, 1.2599) birbirlerinden çok farklı olmadıkları halde müzikteki önemlerinin büyüklüğü dikkate değer.
Seyir Olgusuna Hesaplamalı Bir Yaklaşım
Bu bölümde, tümüyle uygulamalı matematik kapsamına giren özgün bir yöntem özetlenmektedir.
Türk makam müziğinde sözü en sık geçen kavramlardan biri seyirdir. Bir müzik eseri boyunca an an hangi notaların hangi sürelerle seslendirildiği biçiminde açıklanabilecek bu olgu, makam kavramının tanımında temel bir yer tutar. Ezgilerin yürüyüş çizgileri kategorize edilerek seyirler üç türe indirgenir ve her bir makamın seyri bu şemalardan biriyle eşleştirilir:
1. Çıkıcı, 2. İnici, 3. Çıkıcı / İnici.
Açıklayacağımız yöntem seyir olgusunu istatistik / geometrik yöntemlerle hesaplayıp ondan çıkarımlar yapmaya yöneliktir. Bu yöntemin ilk adımı önce15 bir makam müziği özniteliği olarak dile getirilmiş, daha sonra16 ayrıntılandırılmıştır.
Yöntemi uygulamak için ilk olarak, karşılaştırılacak makamlardaki eserlerin tek tek ortalama seyir karakterleri belirlenir. Bunun için eserler süre olarak belirli bir sayıda (genellikle 32) dilime bölünür ve her bir dilimdeki perdelerin frekans ortalamaları hesaplanır (Doğrusal değerlerle çalışmak için, frekanslar sabit bir referans perdesi ile koma cinsinden logaritmik müzikal aralıklar birimine dönüştürülerek işlem yapılmıştır). Hesaplamalarda eserlerin notaları (sembolik veriler) kullanılmıştır. Fakat aynı yöntem icraların frekans analizleri yapılmak suretiyle o verilere de uygulanabilir.
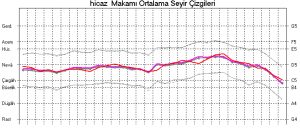
Şekil 10’da, SymbTr17 veritabanındaki Hicaz makamından 223 adet eserin ortalama seyir çizgileri görülmektedir.
Şekil 10. Hicaz makamında 223 adet eserin ortalama seyir çizgileri: Ortalama (mavi) [ve standart sapmalar (siyah)], ağırlıklı ortalama (yeşil), medyan (mor), mod (kırmızı)
Literatürde bu makamın inici seyir karakterine sahip olduğu yazılıdır. Şekil bunu kısmen doğrular niteliktedir. Çünkü seyir tiz bölgeden başlamaktadır.
Bu kez Hüzzam makamındaki 165, Segâh makamındaki 112 eserden elde edilen ortalama seyir çizgilerini bir arada gösterelim (bkz. Şekil 11).
Şekil 11. Hüzzam (mavi), Segâh (kırmızı) ortalama seyir çizgileri
Literatürde her iki makamın da çıkıcı seyir karakterine sahip olduğu yazılıdır ve bu, şekilde de görülebilmektedir. Ayrıca Hüzzam makamının daha tiz bir seyir bölgesine sahip olduğu belirgindir.
Bu makalede ilk kez dile getirilen konu ise, iki seyir çizgisinin uzaklığı kavramıdır. Şöyle hesaplanır:
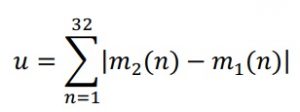 Burada m1 ve m2 dizileri, iki makamın her bir dilimdeki tonlama ortalamalarını göstermektedir.
Burada m1 ve m2 dizileri, iki makamın her bir dilimdeki tonlama ortalamalarını göstermektedir.
Şekil 11’de grafiği görülen Hüzzam ve Segâh makamları seyir çizgileri için çeşitli uzaklıklar hesaplanınca şu değerler elde edilir (bkz. Tablo 1):
Tablo 1. Hüzzam ile Segâh makamlarının çeşitli yöntemlere göre birbirlerine uzaklıkları

Âhenk kavramı ve minimum uzaklık
Müzikte notaların frekansları değil, ardışık ya da andaş notaların frekanslarının oranları önemlidir. Teksesli bir müzik olan Türk musikisinde bir eserin aralık yapısı bozulmadan pes ya da tiz bölgelerde icra edilebilmesi gibi bir gelenek vardır ve bu olguya âhenk denilir. Bir eser iki farklı âhenkte icra edildiğinde, sesin pesliği/tizliği dışında aynı ezgi algılanır. Dolayısıyla uzaklık tanımı yapılırken bu olgunun dikkate alınmasında yarar vardır. Bu yeni tanıma göre, aynı bir eserin iki farklı âhenkteki icrasının birbirlerine uzaklıkları 0 (sıfır) olacaktır.
Minimum uzaklık, karşılaştırılacak iki seyir çizgisinden biri sabit tutulup öteki birer komalık adımlarla kaydırılmak ve her adımda uzaklıkları hesaplamak, sonunda da bu uzaklıkların minimumu seçilmek suretiyle elde edilir. Bu işlemin matematik ifadesi şöyledir:

Şekil 11’deki Hüzzam ile Segâh makamları seyir çizgileri için bu işlem yapılırsa Tablo 2’deki sonuçlar elde edilir.
Tablo 2. Hüzzam ile Segâh makamlarının çeşitli yöntemlere göre birbirlerine ötelemeli (minimum) uzaklıkları

Bambaşka iki makamın birbirine uzaklığı için ne tür sonuçlar çıkabileceğine örnek olmak üzere, yukarıda verilen Hüzzam makamı ile Hüseynî makamında 103 eserden elde edilen verilerle seyir çizgileri grafiği oluşturulmuştur (bkz. Şekil 12).
Şekil 12. Hüzzam (223 eser ortalaması) ile Hüseynî (103 eser ortalaması) makamlarının seyir çizgileri
Bu veriler için normal ve minimum (ötelemeli) uzaklık hesaplama işlemlerinin sonuçları da Tablo 3’tedir.
Tablo 3. Hüzzam ile Hüseynî makamlarının çeşitli yöntemlere göre birbirlerine uzaklıkları
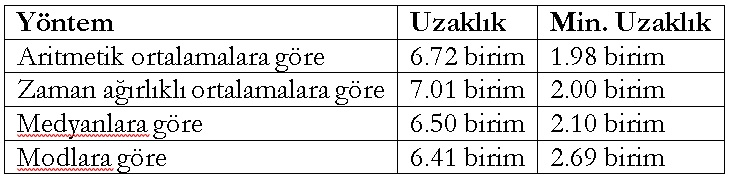
Görüldüğü gibi hem normal hem minimum uzaklıklar bakımından her tür ortalamaya göre hesaplanan ve Tablo 3’te toplanan değerler, Tablo 1 ve Tablo 2’deki karşılık gelen değerlerden büyüktür. Yani Hüzzam makamı Segâh makamına, Hüseynî makamına olduğundan daha yakındır.
Bu yöntemle
- İki eser arasındaki uzaklık,
- Bir makam ile bir eser arasındaki uzaklık
da hesaplanabilir. Böylelikle herhangi iki eserin birbirine benzerliği ve bir eserin bir makamı ne derece temsil ettiği gibi bilgilerin sayısal değerlerle ifade edilebilme olanağı doğar.
Kaynakça
Bianchini, R., Cipriani, A., & Di Scipio, A. 2000. Virtual Sound: Sound Synthesis and Signal Processing, Theory and Practice with Csound: ConTempo.
Bozkurt, B., Karaosmanoğlu, M. K., & Dişiaçık, N. D. 2014. “A computational approach to representing melodic progression (seyir) for Turkish makam music. ” 3rd International Conference on Analytical Approaches to World Music (AAWM), s. 1–2 :London.
Green, D. H., Benson, R. L., Constable, G., & Lanham, C. D. 2007. “Renaissance and Renewal in the Twelfth Century.” The Modern Language Review: https://doi.org/10.2307/3729298.
Haynes, B. 2002. A history of performing pitch: the story of’A’:Scarecrow Press.
Karadeniz, M. E. 1983. Türk Musıkisinin Nazariye ve Esasları.İstanbul: İş Bankası Yayınları.
Karaosmanoğlu, M. K. 2012. “A Turkish makam music symbolic database for music information retrieval: Symbtr.” Proceedings of the 13th ISMIR Conference, 1(13) , 223–228: Porto, Portugal, . http://compmusic.upf.edu/system/files/static_files/KemalKaraosmanoglu_Ismir2012.pdf
Karaosmanoğlu, M. K. 2017. Müzik Aritmetiği ve Ses Sistemleri. İstanbul: İTÜ Vakfı Yayınları.
Kütük, B. Ş., & Şahin, M. 2017. “Fizik Alanındaki Gelişmelerin Sosyolojiye Yansımaları: Pozitivizm.” Sosyoloji Konferansları, (56), s.183.
Rossing, T. D., Moore, F. R., & Wheeler, P. A. 1990. The science of sound (Vol. 2):Addison-Wesley Reading, MA.
Sethares, W. A. 2005. Tuning, timbre, spectrum, scale (Vol. 2): Springer.
Turabi, A.H. 2009. İbn Sînâ ve Müzik. Uluslararası İbn Sînâ Sempozyumu. İstanbul
Ünal, E., Bozkurt, B., & Karaosmanoğlu, M. K. 2012. “Incorporating Features Of Distribution And Progression For Automatic Makam Classification.” 2nd CompMusic Workshop, s. 43–47:Istanbul.
Uzdilek, S. M. 1977. İlim ve mûsikî: Türk mûsikîsi üzerinde incelemeler (Vol. 267):Kültür Bakanlığı, Devlet Kitapları Müdürlüğü.
Notlar
- Bu yazı, yazarın 21 – 22 Haziran 2019 tarihleri arasında Marmara Üniversitesi tarafından İstanbul’da düzenlenen Disiplinlerarası Yaklaşımda Uluslararası Matematik ve Müzik Kongresi’ndeki (DYUMM) davetli konuşmasının genişletilmiş şeklidir.
- Green, Benson, Constable, & Lanham, 2007
- (Yazar tarafından önemi vurgulanmıştır.) Kütük & Şahin, 2017
- a.g.e.
- Turabi, 2009,204
- Haynes, 2002
- Rossing, Moore, & Wheeler, 1990
- Karaosmanoğlu, 2017,201
- Bianchini, Cipriani, & Di Scipio, 2000,68
- Uzdilek, 1977.
- Karadeniz, 1965.
- Eşit tamperamanlı sistemler, bünyesindeki notalar frekanslarına göre sıralandığında, ardışık notaların oluşturduğu müzikal aralıkların eşit olduğu sistemlerdir. Bunlardan dünyada en yaygın olanı 12 ton eşit tamperaman (12TET) sistemidir. Bu sistemdeki ardışık notaların bağıl frekansları
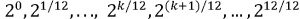 şeklindedir. Dolayısıyla dizideki her bir sesin bağıl frekansı bir önceki sesin bağıl frekansına bölününce
şeklindedir. Dolayısıyla dizideki her bir sesin bağıl frekansı bir önceki sesin bağıl frekansına bölününce 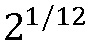 sayısı elde edilir.
sayısı elde edilir. - Sethares, 2005,329
- Bu paragrafta sözü geçen üç sistemin La’sı da 440 Hz olarak alındığı için, yalnızca Fa notasının üç farklı frekansından söz edilmiştir. Gerçekte herhangi bir referans nota söz konusu olmasa da burada yazanlar geçerlidir. Ancak o takdirde Fa ile La’nın frekanslarından değil, Fa – La müzikal aralığından söz etmek gerekir:
Pisagor sisteminde 4.08 yarı-ton
Fark 0.22 yarı-ton
Zarlino “ 3.86 “
Fark 0.14
12TET “ 4 “
Görüldüğü gibi 12TET’in büyük üçlü aralığı doğal büyük üçlü aralığına, Pisagor büyük üçlüsü aralığından daha yakındır (0.22 – 0.14 = 0.08 yarı-ton).
- Ünal, Bozkurt, & Karaosmanoğlu,2012
- Bozkurt, Karaosmanoğlu, & Dişiaçık,2014
- Karaosmanoğlu, 2012



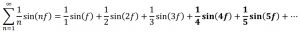



Yorum Bırak